Pýþagórasarsetningin

Hér er persóna sem gerir mikið af nemendum á miðstigi á hverju ári í miklum vandræðum, en einnig kennurum.

Reyndar skildi þessi maður eftir okkur setningu fyrir löngu síðan og á hverju ári reyna margir nemendur að skilja og muna jöfnu hans.

Frá ári til árs verða kennarar þínir að hjálpa þér að uppgötva, skilja og læra þessa setningu.

Ég vil tala hér um Pýþagóras.

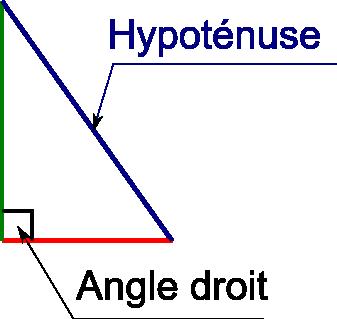
THE Pýþagóras setning má orða það svo: „ Í rétthyrndum þríhyrningi er ferningur undirstúku jafnt summu ferninga hinna tveggja hliðanna.”

L’ Hypotenuse táknar í rétthyrndur þríhyrningur, THE gagnstæða hlið hjárétt horn.

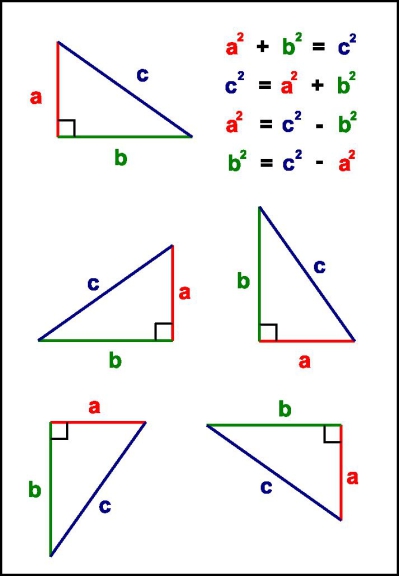
Þú getur tekið eftir því að sama í hvaða átt þríhyrningurinn okkar er, þá breytist jöfnan ekki, en á hinn bóginn er hægt að skrifa hana á mismunandi vegu.

Eftir er að ákvarða hvernig á að finna töluna sem margfaldað með sjálfri sér gefur niðurstöðuna sem finnast í jöfnunni. (Kvaðratrótin)

a x a = a²

b x b = b²

c x c = c²

Ef þú hefur ekki enn farið yfir hvernig á að reikna út a ferningsrót, taktu reiknivélina þína og ýttu á takkann ferningsrót táknað með þessu tákni √

Dæmi til að skilja þessa setningu.

a = 3

b = 4

c =?

Við vitum því að: a² + b² = c²

a² = 3² = 3 x 3 = 9

b² = 4² = 4 x 4 = 16

a² + b² = c²
9 + 16 = 25

c² = 25

c x c = 25

c = 5